NIGMS supports a wide range of research, training, workforce development, and institutional capacity building grants in the biomedical sciences. While NIH’s Center for Scientific Review reviews the majority of our investigator-initiated research grants (read our post on NIGMS RPGs), NIGMS has its own scientific review branch (SRB) that manages the review of applications to programs in workforce development and in research capacity building (past posts on training and capacity building provide more information). These programs often require reviewers with unique experiences, in addition to scientific or technical expertise. Thus, SRB is always searching for volunteers with varying experiences and scientific expertise from all career stages, funding and review experiences, geographic locations, and institution types to provide expert reviews. Some examples include individuals familiar with research training programs, institutional administration, faculty mentorship, Tribal communities, and people with experience conducting research in states that are eligible for Institutional Development Awards.
Continue reading “Volunteer as a Peer Reviewer for NIGMS!”Tag: Peer Review Process
Long-Time Scientific Review Chief Helen Sunshine Retires
 Helen Sunshine, who led the NIGMS Office of Scientific Review (OSR) for the last 27 years, retired in April. Throughout her career, she worked tirelessly to uphold the highest standards of peer review.
Helen Sunshine, who led the NIGMS Office of Scientific Review (OSR) for the last 27 years, retired in April. Throughout her career, she worked tirelessly to uphold the highest standards of peer review.
Helen earned a Ph.D. in chemistry at Columbia University and joined the NIH intramural program in 1976, working first as a postdoctoral fellow and then as a senior research scientist in the Laboratory of Chemical Physics, headed by William Eaton.
In 1981, Helen became a scientific review officer (SRO) in OSR and was appointed by then-NIGMS Director Ruth L. Kirschstein to be its chief in 1989. During her career in OSR, she oversaw the review of many hundreds of applications each year representing every scientific area within the NIGMS mission.
Continue reading “Long-Time Scientific Review Chief Helen Sunshine Retires”
Talking to NIH Staff About Your Application and Grant: Who, What, When, Why and How
Update: Revised content in this post is available on the NIGMS webpage, Talking to NIH Staff About Your Application and Grant.
During the life of your application and grant, you’re likely to interact with a number of NIH staff members. Who’s the right person to contact—and when and for what? Here are some of the answers I shared during a presentation on communicating effectively with NIH at the American Crystallographic Association annual meeting. The audience was primarily grad students, postdocs and junior faculty interested in learning more about the NIH funding process.
Who?
The three main groups involved in the application and award processes—program officers (POs), scientific review officers (SROs) and grants management specialists (GMSs)—have largely non-overlapping responsibilities. POs advise investigators on applying for grants, help them understand their summary statements and provide guidance on managing their awards. They also play a leading role in making funding decisions. Once NIH’s Center for Scientific Review (CSR) assigns applications to the appropriate institute or center and study section, SROs identify, recruit and assign reviewers to applications; run study section meetings; and produce summary statements following the meetings. GMSs manage financial aspects of grant awards and ensure that administrative requirements are met before issuing a notice of award.
How do you identify the right institute or center, study section and program officer for a new application? Some of the more common ways include asking colleagues for advice and looking at the funding sources listed in the acknowledgements section of publications closely related to your project. NIH RePORTER is another good way to find the names of POs and study sections for funded applications. Finally, CSR has information on study sections, and individual institute and center websites, including ours, list contacts by research area. We list other types of contact information on our website, as well.
Becoming a Peer Reviewer for NIGMS
NIH’s Center for Scientific Review (CSR) is not the only locus for the review of grant applications–every institute and center has its own review office, as well. Here at NIGMS, the Office of Scientific Review (OSR) handles applications for a wide variety of grant mechanisms and is always seeking outstanding scientists to serve as reviewers. If you’re interested in reviewing for us, here’s some information that might help.
Why Overall Impact Scores Are Not the Average of Criterion Scores
One of the most common questions that applicants ask after a review is why the overall impact score is not the average of the individual review criterion scores. I’ll try to explain the reasons in this post.
What is the purpose of criterion scores?
Criterion scores assess the relative strengths and weaknesses of an application in each of five core areas. For most applications, the core areas are significance, investigator(s), innovation, approach and environment. The purpose of the scores is to give useful feedback to PIs, especially those whose applications were not discussed by the review group. Because only the assigned reviewers give criterion scores, they cannot be used to calculate a priority score, which requires the vote of all eligible reviewers on the committee.
How do the assigned reviewers determine their overall scores?
The impact score is intended to reflect an assessment of the “likelihood for the project to exert a sustained, powerful influence on the research
field(s) involved.” In determining their preliminary impact scores, assigned reviewers are expected to consider the relative importance of each scored review criterion, along with any additional review criteria (e.g., progress for a renewal), to the likely impact of the proposed research.
The reviewers are specifically instructed not to use the average of the criterion scores as the overall impact score because individual criterion scores may not be of equal importance to the overall impact of the research. For example, an application having more than one strong criterion score but a weak score for a criterion critical to the success of the research may be judged unlikely to have a major scientific impact. Conversely, an application with more than one weak criterion score but an exceptionally strong critical criterion score might be judged to have a significant scientific impact. Moreover, additional review criteria, although not individually scored, may have a substantial effect as they are factored into the overall impact score.
How is the final overall score calculated?
The final impact score is the average of the impact scores from all eligible reviewers multiplied by 10 and then rounded to the nearest whole number. Reviewers base their impact scores on the presentations of the assigned reviewers and the discussion involving all reviewers. The basis for the final score should be apparent from the resume and summary of discussion, which is prepared by the scientific review officer following the review.
Why might an impact score be inconsistent with the critiques?
Sometimes, issues brought up during the discussion will result in a reviewer giving a final score that is different from his/her preliminary score. If this occurs, reviewers are expected to revise their critiques and criterion scores to reflect such changes. Nevertheless, an applicant should refer to the resume and summary of discussion for any indication that the committee’s discussion might have changed the evaluation even though the criterion scores and reviewer’s narrative may not have been updated. Recognizing the importance of this section to the interpretation of the overall summary statement, NIH has developed a set of guidelines to assist review staff in writing the resume and summary of discussion, and implementation is under way.
If you have related questions, see the Enhancing Peer Review Frequently Asked Questions.
Editor’s Note: In the third section, we deleted “up” for clarity.


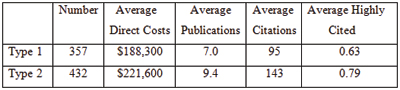
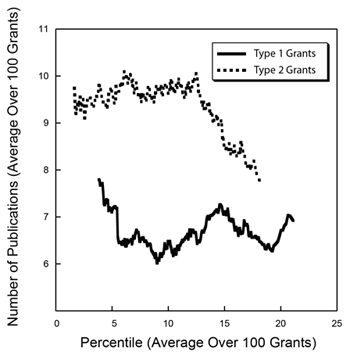
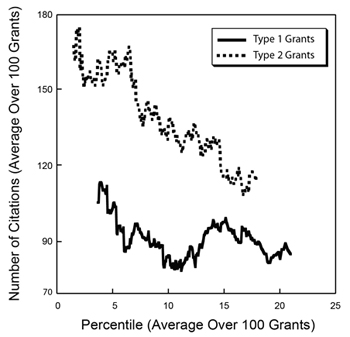
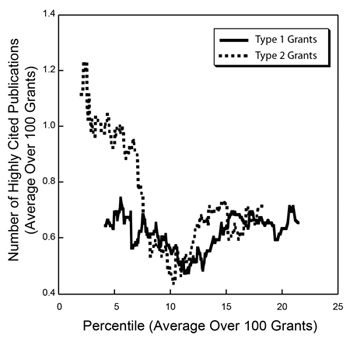
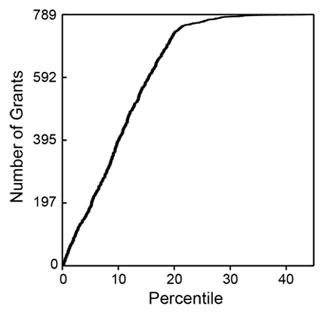
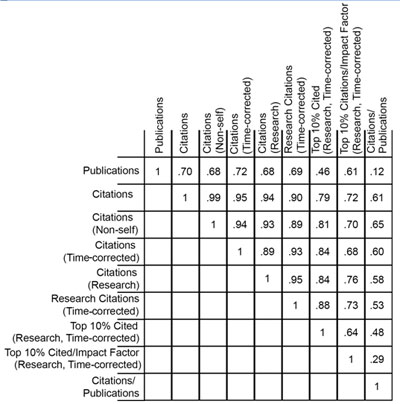
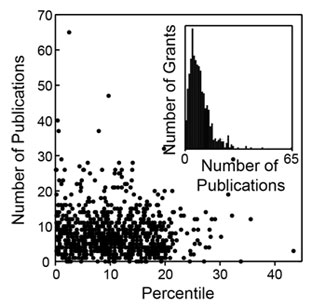
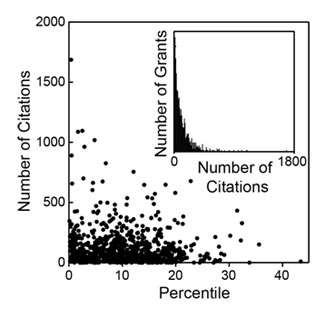

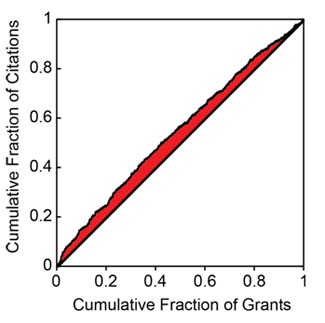
 to plot the cumulative fraction of a given metric as a function of the cumulative fraction of grants, ordered by their percentile scores. Figure 5 shows the Lorentz curve for citations.
to plot the cumulative fraction of a given metric as a function of the cumulative fraction of grants, ordered by their percentile scores. Figure 5 shows the Lorentz curve for citations.